Description
“Let it Bead” company is located upstairs at 700 Cannery Row in Monterey, CA. As you can deduce from the company name, their business is beads. Their PR department found out that customers are interested in buying colored bracelets. However, over 90 percent of the target audience insists that the bracelets be unique. (Just imagine what happened if two women showed up at the same party wearing identical bracelets!) It’s a good thing that bracelets can have different lengths and need not be made of beads of one color. Help the boss estimating maximum profit by calculating how many different bracelets can be produced.
A bracelet is a ring-like sequence of s beads each of which can have one of c distinct colors. The ring is closed, i.e. has no beginning or end, and has no direction. Assume an unlimited supply of beads of each color. For different values of s and c, calculate the number of different bracelets that can be made.
Input
Every line of the input file defines a test case and contains two integers: the number of available colors c followed by the length of the bracelets s. Input is terminated by c=s=0. Otherwise, both are positive, and, due to technical difficulties in the bracelet-fabrication-machine, cs<=32, i.e. their product does not exceed 32.
Output
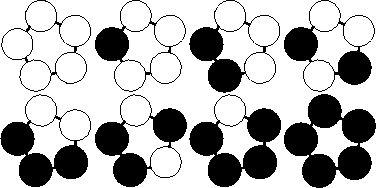
For each test case output on a single line the number of unique bracelets. The figure below shows the 8 different bracelets that can be made with 2 colors and 5 beads.
Sample Input
1 1
2 1
2 2
5 1
2 5
2 6
6 2
0 0
Sample Output
1
2
3
5
8
13
21
题意
c 种颜色的珠子,组成长为 s 的项链,通过旋转或者翻转得到的情况我们算一种,问总共有多少种不同的方案。
思路
Polya 定理的应用
设 $G$ 是 $p$ 个对象的一个置换群,用 $k$ 种颜色去染这 $p$ 个对象,若一种染色方案在群 $G$ 的作用下变成另一种方案,则这两个方案当作是同一种方案,这样的不同染色方案数为:
$$ L=\frac{1}{|G|}×\sum(k^{C(f)}),f\in G $$
其中, $C(f)$ 为置换 $f$ 的循环节个数, $|G|$ 表示群的置换方法数
对于有 $n$ 个位置的项链,有 $n$ 种旋转置换和 $n$ 种翻转置换
对于旋转置换:
$C(f_i)=gcd(n,i)$ , $i$ 表示一次转过 $i$ 颗珠子, $i=0$ 时 $C(f_0)=n$
对于翻转置换:
- 如果 $n$ 为偶数:则有 $\frac{n}{2}$ 个置换 $C(f)=\frac{n}{2}$ (以两条对边中点为轴翻转) ,还有 $\frac{n}{2}$ 个置换 $C(f)=\frac{n}{2}+1$ (以两个对点为轴翻转)
- 如果 $n$ 为奇数: $C(f)=\frac{n}{2}+1$ (以一个点和其对边中点为轴翻转)
AC 代码
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
typedef long long LL;
int gcd(int a,int b)
{
return b?gcd(b,a%b):a;
}
int main()
{
int c,s;
while(~scanf("%d%d",&c,&s)&&(c||s))
{
LL ans=0;
for(int i=1; i<=s; i++)
ans+=pow(c,gcd(s,i));
if(s&1)ans+=s*pow(c,s/2+1);
else ans+=s/2*(pow(c,s/2)+pow(c,s/2+1));
printf("%I64d\n",ans/s/2);
}
return 0;
}