Description
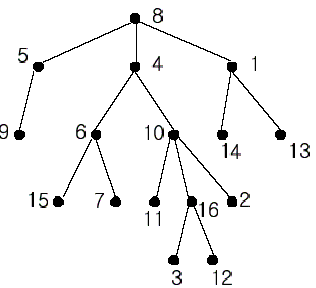
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
In the figure, each node is labeled with an integer from {1, 2,…,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The input consists of T test cases. The number of test cases (T) is given in the first line of the input file. Each test case starts with a line containing an integer N , the number of nodes in a tree, 2<=N<=10,000. The nodes are labeled with integers 1, 2,…, N. Each of the next N -1 lines contains a pair of integers that represent an edge –the first integer is the parent node of the second integer. Note that a tree with N nodes has exactly N – 1 edges. The last line of each test case contains two distinct integers whose nearest common ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2
16
1 14
8 5
10 16
5 9
4 6
8 4
4 10
1 13
6 15
10 11
6 7
10 2
16 3
8 1
16 12
16 7
5
2 3
3 4
3 1
1 5
3 5
Sample Output
4
3
题意
树中有 n 个节点, n-1 条边,现查询节点 a 与节点 b 的最近公共祖先。
思路
因为题中对于一棵树只有一次查询,因此我们有更简单的做法:
- 针对其中的一个节点,沿父路径向上标记至树根。
- 针对另一个节点同样向上标记,直到遇到之前的标记,则此时所在的节点即为这两点最近公共祖先。
标准 LCA 离线做法:
- 选取树中根节点开始 dfs
- 遍历该点 u 所有子节点 v ,并标记这些子节点 v 已被访问过
- 若 v 还存在子节点,返回 2 ,否则下一步
- 合并 v 节点至 u ,此时 u 、 v 属于同一集合
- 寻找与当前点 u 有询问关系的点 v
- 若 v 已经被访问过,则可以确认 u 和 v 的最近公共祖先为 v 被合并到的父亲节点,否则跳过
AC 代码
#include<iostream>
#include<vector>
#include<cstring>
using namespace std;
const int maxn=10001;
int fa[maxn];
int rank[maxn];
int indegree[maxn]; //入度
bool visit[maxn];
vector<int> tree[maxn],Qes[maxn];
int ancestor[maxn];
void init(int n)
{
memset(rank,0,sizeof(rank));
memset(visit,false,sizeof(visit));
memset(indegree,0,sizeof(indegree));
memset(ancestor,0,sizeof(ancestor));
for(int i=1; i<=n; i++)
{
fa[i]=i;
tree[i].clear();
Qes[i].clear();
}
}
int find_set(int x) //并查集 查询+路径压缩
{
if(x!=fa[x])
fa[x]=find_set(fa[x]);
return fa[x];
}
void union_set(int x,int y) //并查集 合并
{
x=find_set(x);
y=find_set(y);
if(rank[x]>rank[y])
fa[y]=x;
else
{
fa[x]=y;
if(rank[x]==rank[y])
rank[y]++;
}
}
void LCA(int u)
{
ancestor[u]=u;
int len = tree[u].size();
for(int i=0; i<len; i++)
{
LCA(tree[u][i]);
union_set(u,tree[u][i]);
ancestor[find_set(u)]=u;
}
visit[u]=true;
len = Qes[u].size();
for(int i=0; i<len; i++)
{
if(visit[Qes[u][i]]) //如果该点之前访问过,输出最近公共祖先
{
cout<<ancestor[find_set(Qes[u][i])]<<endl;
return;
}
}
}
int main()
{
int cnt;
int n;
cin>>cnt;
while(cnt--)
{
cin>>n;;
init(n);
int s,t;
for(int i=1; i<n; i++)
{
cin>>s>>t;
tree[s].push_back(t);
indegree[t]++;
}
cin>>s>>t;
Qes[s].push_back(t);
Qes[t].push_back(s);
for(int i=1; i<=n; i++)
if(!indegree[i])
{
LCA(i);
break;
}
}
return 0;
}