Description
某首都城市的商人要经常到各城镇去做生意,他们按自己的路线去做,目的是为了更好的节约时间。
假设有N个城镇,首都编号为1,商人从首都出发,其他各城镇之间都有道路连接,任意两个城镇之间如果有直连道路,在他们之间行驶需要花费单位时间。该国公路网络发达,从首都出发能到达任意一个城镇,并且公路网络不会存在环。
你的任务是帮助该商人计算一下他的最短旅行时间。
Input Description
输入文件中的第一行有一个整数N,1<=n<=30 000,为城镇的数目。下面N-1行,每行由两个整数a 和b (1<=a, b<=n; a<>b)组成,表示城镇a和城镇b有公路连接。在第N+1行为一个整数M,下面的M行,每行有该商人需要顺次经过的各城镇编号。
Output Description
在输出文件中输出该商人旅行的最短时间。
Sample Input
5
1 2
1 5
3 5
4 5
4
1
3
2
5
Sample Output
7
思路
所有的道路都是双向的,并且没有环,因此我们可以根据边来建树。
如下图(样例):
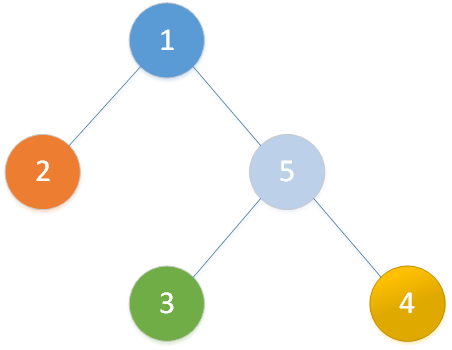
依次经过 1 3 、 3 2 、 2 5 这几条路径,从图中我们可以发现,路径的长度刚好等于两端点与其最近公共祖先的深度差之和。
于是:
1->3: $dep[1]+dep[3]-2×dep[1]=1+3-2=2$
3->2: $dep[2]+dep[3]-2×dep[1]=2+3-2=3$
2->5: $dep[2]+dep[5]-2×dep[1]=2+2-2=2$
然后题目便转化为基础的 LCA 问题咯~
AC 代码
#include<iostream>
#include<vector>
#include<cstring>
#include<cstdio>
using namespace std;
const int maxn=31000;
int fa[maxn];
int rank[maxn];
bool visit[maxn];
vector<int> tree[maxn],Qes[maxn];
int ancestor[maxn];
int ans;
int dep[maxn];
void init(int n)
{
memset(rank,0,sizeof(rank));
memset(visit,false,sizeof(visit));
memset(ancestor,0,sizeof(ancestor));
memset(dep,0,sizeof(dep));
ans=0;
for(int i=1; i<=n; i++)
{
fa[i]=i;
tree[i].clear();
Qes[i].clear();
}
}
int find_set(int x) //并查集 查询+路径压缩
{
if(x!=fa[x])
fa[x]=find_set(fa[x]);
return fa[x];
}
void union_set(int x,int y) //并查集 合并
{
x=find_set(x);
y=find_set(y);
if(rank[x]>rank[y])
fa[y]=x;
else
{
fa[x]=y;
if(rank[x]==rank[y])
rank[y]++;
}
}
void LCA(int u,int pa,int deep)
{
ancestor[u]=u;
dep[u]=deep;
int len = tree[u].size();
for(int i=0; i<len; i++)
{
if(tree[u][i]==pa)continue;
LCA(tree[u][i],u,deep+1);
union_set(u,tree[u][i]);
ancestor[find_set(u)]=u;
}
visit[u]=true;
len = Qes[u].size();
for(int i=0; i<len; i++)
{
if(visit[Qes[u][i]])
ans+=dep[u]+dep[Qes[u][i]]-2*dep[ancestor[find_set(Qes[u][i])]];
}
}
int data[maxn];
int main()
{
int n,m;
while(~scanf("%d",&n))
{
init(n);
for(int i=0; i<n-1; i++)
{
int u,v;
scanf("%d%d",&u,&v);
tree[u].push_back(v);
tree[v].push_back(u);
}
scanf("%d",&m);
for(int i=0; i<m; i++)
{
scanf("%d",data+i);
if(i)
{
Qes[data[i]].push_back(data[i-1]);
Qes[data[i-1]].push_back(data[i]);
}
}
LCA(1,0,1);
printf("%d\n",ans);
}
return 0;
}


