Matrix Again
Time Limit: 5000/2000 MS (Java/Others) Memory Limit: 102400/102400 K (Java/Others)
Total Submission(s): 4196 Accepted Submission(s): 1212
Problem Description
Starvae very like play a number game in the n*n Matrix. A positive integer number is put in each area of the Matrix.
Every time starvae should to do is that choose a detour which from the top left point to the bottom right point and than back to the top left point with the maximal values of sum integers that area of Matrix starvae choose. But from the top to the bottom can only choose right and down, from the bottom to the top can only choose left and up. And starvae can not pass the same area of the Matrix except the start and end..
Do you know why call this problem as “Matrix Again”? AS it is like the problem 2686 of HDU.
Every time starvae should to do is that choose a detour which from the top left point to the bottom right point and than back to the top left point with the maximal values of sum integers that area of Matrix starvae choose. But from the top to the bottom can only choose right and down, from the bottom to the top can only choose left and up. And starvae can not pass the same area of the Matrix except the start and end..
Do you know why call this problem as “Matrix Again”? AS it is like the problem 2686 of HDU.
Input
The input contains multiple test cases.
Each case first line given the integer n (2<=n<=600)
Then n lines, each line include n positive integers. (<100)
Each case first line given the integer n (2<=n<=600)
Then n lines, each line include n positive integers. (<100)
Output
For each test case output the maximal values starvae can get.
Sample Input
2
10 3
5 10
3
10 3 3
2 5 3
6 7 10
5
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
5 6 7 8 9
Sample Output
28
46
80
题意
给出一个 n∗n 的数字矩阵,求从左上角开始到右下角两条不相交路径数值和的最大值,要求以单个点来看,从它出发的路径只能向右或者向下。
比如:
10 3 3
2 5 3
6 7 10
- 第一条路径: 10→3→5→3→10=31
- 第二条路径: 10→2→6→7→10=35
因此最终答案为 31+35−10−10=46
思路
既然我们需要找两条不相交的路径,然后计算这些边的权值和,如果把所有该有的边都加入,构成一张图之后,试想一下,假设所有的边都是一条管道,而管道的容量都为1,而我们刚开始在起点位置注入2的水,这样到终点便有了两条不相交的路径。但是每一个点邻接它右边与下边的点,并且这两条边不能同时有效(除了起点),因为每一个点的数字只能分配给与它相邻的一个点。
如果说这道题难的话就是建图咯!加入一个源点,加入一个汇点,用这两个点邻接边的容量来描述图中路径的个数。
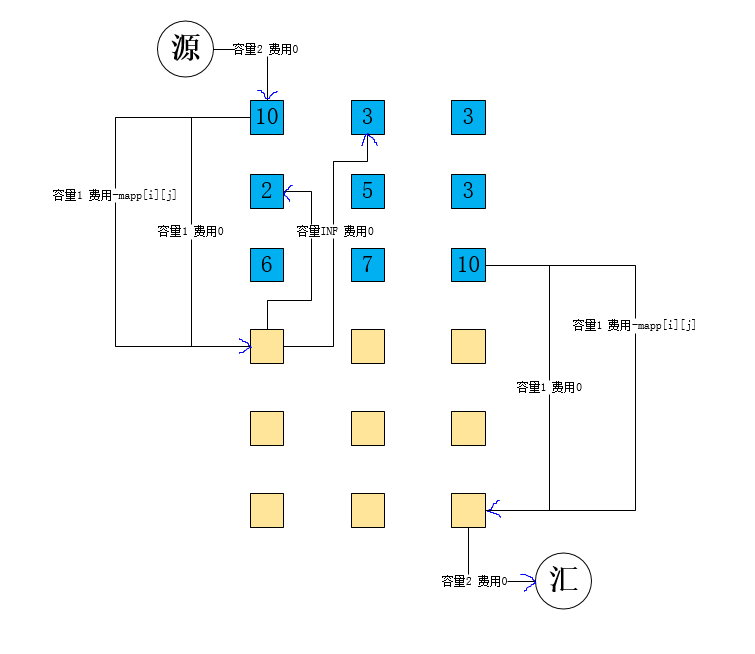
第一次为一篇文章去画图,画的好难看,只画出了第一个点的建图模型,其他的类似,具体的看代码咯!
AC代码:
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<vector>
#include<queue>
using namespace std;
const int MAXX = 800010;
const int INF = 0x3f3f3f3f;
struct edge
{
int to; //边终点
int next; //下一个兄弟位置
int cap; //容量
int flow; //流量
int cost; //费用
} edge[MAXX<<2];
int head[MAXX],tol;
int pre[MAXX],dis[MAXX];
int N; //节点总个数
void init(int n)
{
N=n;
tol=0;
memset(head,-1,sizeof(head));
}
void addedge(int u,int v,int cap,int cost) //同时增加原边与反向边
{
edge[tol].to=v;
edge[tol].cap=cap;
edge[tol].cost=cost;
edge[tol].flow=0;
edge[tol].next=head[u];
head[u]=tol++;
edge[tol].to=u;
edge[tol].cap=0;
edge[tol].cost=-cost;
edge[tol].flow=0;
edge[tol].next=head[v];
head[v]=tol++;
}
/*
* SPFA 算法判断是否存在s到t的通路
*/
bool spfa(int s,int t)
{
queue<int>q;
bool vis[MAXX];
for(int i=0; i<N; i++)
{
dis[i]=INF;
vis[i]=false;
pre[i]=-1;
}
dis[s]=0;
vis[s]=true;
q.push(s);
while(!q.empty())
{
int u=q.front();
q.pop();
vis[u]=false;
for(int i=head[u]; i!=-1; i=edge[i].next) //遍历所有与u临接的点
{
int v=edge[i].to;
if(edge[i].cap>edge[i].flow&&dis[v]>dis[u]+edge[i].cost) //如果可以松弛该点
{
dis[v]=dis[u]+edge[i].cost;
pre[v]=i;
if(!vis[v]) //如果该点不在队列中,入队
{
vis[v]=true;
q.push(v);
}
}
}
}
return (pre[t]!=-1); //返回是否s到t是否有路径
}
/*
* int s 起点
* int t 终点
* 返回费用cost
*/
int minCostMaxFlow(int s,int t)
{
int cost=0;
while(spfa(s,t))
{
int minn=INF; //当前路径可增广值
for(int i=pre[t]; i!=-1; i=pre[edge[i^1].to]) //因为建图时每增加一条边会同时加入它的反向边,因此i^1为找出与i刚好相反的部分
{
if(minn>edge[i].cap-edge[i].flow)
minn=edge[i].cap-edge[i].flow;
}
for(int i=pre[t]; i!=-1; i=pre[edge[i^1].to]) //修改图,计算花费
{
edge[i].flow+=minn;
edge[i^1].flow-=minn;
cost+=edge[i].cost*minn;
}
}
return cost;
}
int main()
{
int n;
int mapp[605][605];
while(~scanf("%d",&n))
{
int k=n*n;
int t=2*k+1;
init(t+1);
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
{
scanf("%d",&mapp[i][j]);
addedge(j+(i-1)*n,j+(i-1)*n+k,1,-mapp[i][j]);
if(j!=n)addedge(k+j+(i-1)*n,j+1+(i-1)*n,INF,0);
if(i!=n)addedge(k+j+(i-1)*n,i*n+j,INF,0);
}
addedge(0,1,2,0);
addedge(1,k+1,1,0);
addedge(t-1,t,2,0);
addedge(k,t-1,1,0);
printf("%d\n",-minCostMaxFlow(0,t));
}
return 0;
}


