Description
Wherever the destination is, whoever we meet, let’s render this song together.
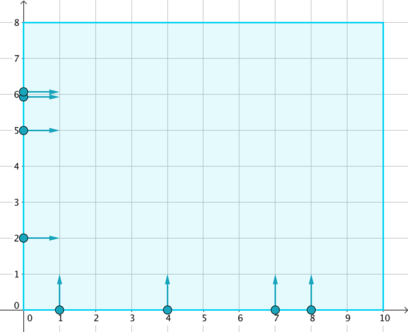
On a Cartesian coordinate plane lies a rectangular stage of size w × h, represented by a rectangle with corners (0, 0), (w, 0), (w, h) and (0, h). It can be seen that no collisions will happen before one enters the stage.
On the sides of the stage stand n dancers. The i-th of them falls into one of the following groups:
- Vertical: stands at (xi, 0), moves in positive y direction (upwards);
Horizontal: stands at (0, yi), moves in positive x direction (rightwards).
According to choreography, the i-th dancer should stand still for the first ti milliseconds, and then start moving in the specified direction at 1 unit per millisecond, until another border is reached. It is guaranteed that no two dancers have the same group, position and waiting time at the same time.
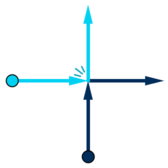
When two dancers collide (i.e. are on the same point at some time when both of them are moving), they immediately exchange their moving directions and go on.
Dancers stop when a border of the stage is reached. Find out every dancer’s stopping position.
Input
The first line of input contains three space-separated positive integers n, w and h (1 ≤ n ≤ 100 000, 2 ≤ w, h ≤ 100 000) — the number of dancers and the width and height of the stage, respectively.
The following n lines each describes a dancer: the i-th among them contains three space-separated integers gi, pi, and ti (1 ≤ gi ≤ 2, 1 ≤ pi ≤ 99 999, 0 ≤ ti ≤ 100 000), describing a dancer’s group gi (gi = 1 — vertical, gi = 2 — horizontal), position, and waiting time. If gi = 1 then pi = xi; otherwise pi = yi. It’s guaranteed that 1 ≤ xi ≤ w - 1 and 1 ≤ yi ≤ h - 1. It is guaranteed that no two dancers have the same group, position and waiting time at the same time.
Output
Output n lines, the i-th of which contains two space-separated integers (xi, yi) — the stopping position of the i-th dancer in the input.
Examples input
8 10 8
1 1 10
1 4 13
1 7 1
1 8 2
2 2 0
2 5 14
2 6 0
2 6 1
Examples output
4 8
10 5
8 8
10 6
10 2
1 8
7 8
10 6
Hint
样例解释
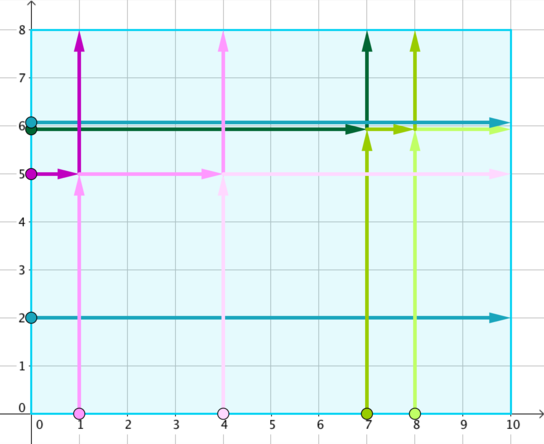
题意
场上有 $n$ 个点,它们分别向上与向右在不同时刻开始运动,相遇则改变移动方向,求最终这些点到达的坐标。
思路
设有一点 $a$ 在 $x$ 轴的坐标为 $(x_1,0)$ , $t_1$ 时间后出发。
设有一点 $b$ 在 $y$ 轴的坐标为 $(0,y_2)$ , $t_2$ 时间后出发。
若 $a,b$ 相遇,则 $y_2+t_1=x_1+t_2$ ,即 $x_1-t_1=y_2-t_2$ 。
我们来看样例中的 $(1,1,10),(1,4,13),(2,5,14)$ 这三个点,显然理论无影响下 $(2,5,14)$ 会与另外两个点相遇。
从 hint 中我们可以看出, $(1,1,10)$ 在与 $(2,5,14)$ 相遇后改变了移动方向,随后又与 $(1,4,13)$ 相遇而改变方向,最终,只有最右侧可以相遇的点没有受到其他影响。
我们称这样的碰撞为方向的传递,即 $(2,5,14)$ 将其移动方向传递给了 $(1,4,13)$ ,而对中间过渡的那些点不做考虑。
显然,我们首先应该对 $x$ 轴与 $y$ 轴上的这些点根据其距离原点的位置从小到大排序。
对于 $x$ 轴每一点的时刻 $x_i-t_i$ 我们维护一个队列,队列里记录满足该时刻点的标号,按横坐标大小排序。
而对 $y$ 轴的这些点中,我们去查找队列 $y_i-t_i$ :
- 若为空,则说明没有任何一个点会影响该点的运动
- 否则将当前点的移动状态转移给队列尾部的那一个点,然后将自身加入该队列的首部。(因为最后只有自身与队尾改变了移动方向)
所有最终出现在 $x=w$ 上点的坐标这样就可以确定了,同理出现在 $y=h$ 上的点也是一样的方法。
AC 代码
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
typedef __int64 LL;
typedef map<int,deque<int> >::iterator MPIT;
map<int,deque<int> > mapp;
int n,w,h;
int ax[maxn],ay[maxn],tmp[maxn];
struct node
{
int gg,pp,tt,id;
bool operator<(const node &x)const
{
return pp<x.pp;
}
} a[maxn];
void call(int cal,int o)
{
for(int i=1; i<=n; ++i)
if(a[i].gg==cal)
mapp[a[i].tt-a[i].pp].push_back(i);
for(int i=1; i<=n; ++i)
if(a[i].gg==o)
{
MPIT it=mapp.find(a[i].tt-a[i].pp);
if(it==mapp.end() || it->second.empty())
tmp[i]=i;
else
{
tmp[i]=it->second.back();
it->second.pop_back();
it->second.push_front(i);
}
}
mapp.clear();
}
void solve()
{
sort(a+1,a+n+1);
call(1,2);
call(2,1);
for(int i=1; i<=n; i++)
if(a[i].gg==1)
{
ax[a[tmp[i]].id]=a[i].pp;
ay[a[tmp[i]].id]=h;
}
else
{
ax[a[tmp[i]].id]=w;
ay[a[tmp[i]].id]=a[i].pp;
}
for(int i=1; i<=n; i++)
cout<<ax[i]<<" "<<ay[i]<<endl;
}
int main()
{
ios::sync_with_stdio(false);
cin>>n>>w>>h;
for(int i=1; i<=n; i++)
cin>>a[i].gg>>a[i].pp>>a[i].tt,a[i].id=i;
solve();
return 0;
}