Description
A cellular automaton is a collection of cells on a grid of specified shape that evolves through a number of discrete time steps according to a set of rules that describe the new state of a cell based on the states of neighboring cells. The order of the cellular automaton is the number of cells it contains. Cells of the automaton of order n are numbered from 1 to n.
The order of the cell is the number of different values it may contain. Usually, values of a cell of order m are considered to be integer numbers from 0 to m−1.
One of the most fundamental properties of a cellular automaton is the type of grid on which it is computed. In this problem we examine the special kind of cellular automaton — circular cellular automaton of order n with cells of order m. We will denote such kind of cellular automaton as n,m − automaton.
A distance between cells i and j in n,m-automaton is defined as min(|i − j|,n −|i − j|). A denvironment of a cell is the set of cells at a distance not greater than d.
On each d-step values of all cells are simultaneously replaced by new values. The new value of cell i after d-step is computed as a sum of values of cells belonging to the d-enviroment of the cell i modulo m.
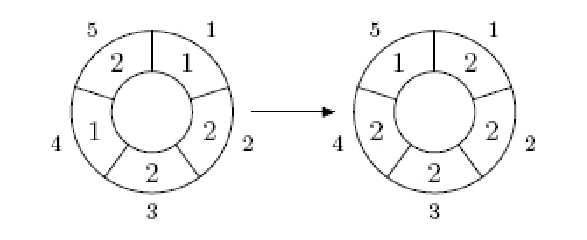
The following picture shows 1-step of the 5,3-automaton.
Input
The input file contains several test cases, each of them consists of two lines, as described below.
The first line of the input contains four integer numbers n, m, d, and k (1 ≤ n ≤ 500, 1 ≤ m ≤ 1000000, 0 ≤ d < n 2 , 1 ≤ k ≤ 10000000).
The second line contains n integer numbers from 0 to m−1 — initial values of the automaton’s cells.
Output
For each test case, write to the output, on a line by itself, the values of the n,m-automaton’s cells after k d-steps.
Sample Input
5 3 1 1
1 2 2 1 2
5 3 1 10
1 2 2 1 2
Sample Output
2 2 2 2 1
2 0 0 2 2
题意
一个细胞自动机包含 n 个格子,每个格子的取值为 (0,m) ,给定距离 d ,每次操作后每个格子的值变为与它的距离不超过 d 的所有格子在操作前的值之和模 m ,计算 k 次操作后各格子的值。
思路
我们把经过 k 次操作后各格子的值看作列向量 $V_{k}$ ,不难发现 $V_k$ 可以用 $V_{k-1}$ 通过某种变换求得,而这种变换便是 $V_{k-1}$ 中相邻 $2×d+1$ 个元素的和模 m 。
于是整个变换可以通过矩阵乘法来描述
设 $V_0$ 为初始列向量,当 $d=1$ 时:
$$ \begin{equation} A =\begin{bmatrix} 1&1&0& \cdots\ &0&1 \\ 1&1&1&0&\cdots\ & 0 \\ 0&1&1&1&0&\cdots\ \\ \cdots\ &0&1&1&1&0 \\ 1&\cdots\ &0&0&1&1 \\ 1&1&\cdots\ &0&0&1 \\ \end{bmatrix} \end{equation} $$
最终答案: $V_k=A^kV_0$
其中 $A^k$ 可以使用矩阵快速幂来求得,时间复杂度 $O(n^3\log k)$ ,会超时。
注意这一个矩阵是循环矩阵,而循环矩阵之间的乘积仍然是循环矩阵,于是我们可以只存储矩阵的一行,计算的时候也只计算这一行即可,时间复杂度 $O(n^2\log k)$ 。
AC 代码
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n,m,d,k;
LL np[500][500];
int idx=0;
struct marx
{
int tot;
marx()
{
tot=idx++;
}
marx mult(const marx&a,const marx&b)
{
marx ans = marx();
for(int i=0; i<n; i++)
{
LL num=0;
for(int j=0; j<n; j++)
{
num=(num+(np[a.tot][(j-i+n)%n]*np[b.tot][j])%m)%m;
}
np[ans.tot][i]=num;
}
return ans;
}
marx mul(const marx&a,const marx&b)
{
marx ans=marx();
for(int i=0; i<n; i++)
for(int j=0; j<n; j++)
np[ans.tot][i]=(np[ans.tot][i]+(np[a.tot][j]*np[b.tot][(j-i+n)%n])%m)%m;
return ans;
}
};
marx mult(marx a,LL n)
{
marx ans=marx();
np[ans.tot][0]=1;
while(n)
{
if(n&1)ans=ans.mul(ans,a);
a=a.mul(a,a);
n>>=1;
}
return ans;
}
int main()
{
ios::sync_with_stdio(false);
while(cin>>n>>m>>d>>k)
{
memset(np,0,sizeof(np));
idx=0;
marx ans = marx();
for(int i=0; i<n; i++)
cin>>np[ans.tot][i];
marx ap = marx();
for(int j=-d; j<=+d; j++)
np[ap.tot][(j+n)%n]=1;
ans=ans.mult(mult(ap,k),ans);
for(int i=0; i<n; i++)
cout<<np[ans.tot][i]<<((i!=n-1)?" ":"\n");
}
return 0;
}