RMQ (Range Minimum/Maximum Query),即区间最值问题。
对于长度为 n 的数列 A ,回答若干查询 RMQ(A,i,j)(i,j<=n) ,返回数列 A 中下标在 i,j 里的最大(小)值。
相关算法
- 朴素(搜索),时间复杂度: $O(n)-O(q×n)$ ,online
- 线段树,时间复杂度: $O(n)-O(q×\log n)$ ,online
- ST(动态规划),时间复杂度: $O(n×\log n)-O(q)$ ,online
- RMQ标准算法,先规约为 LCA ,再规约成约束 RMQ ,时间复杂度: $O(n)-O(q)$ ,online
ST 算法
假设当前题目要求区间最小值,我们令 dp[i][j] 代表从 i 开始,长度为 $2^j$ 这段区间的最小值。
于是便有: $dp[i][j]=\min(dp[i][j-1],dp[i+2^{j-1}][j-1])$
分析可知, $dp[i][j-1]$ 代表从 i 开始,长度为 $2^j$ 区间一半中的最小值,而 $dp[i+2^{j-1}][j-1]$ 即为区间的另一半。
最终(从下往上看):
| dp[0][*] | dp[1][*] | dp[2][*] | dp[3][*] | dp[4][*] | dp[5][*] | dp[6][*] | dp[7][*] | |
|---|---|---|---|---|---|---|---|---|
| dp[*][3] | 1 | |||||||
| dp[*][2] | 1 | 1 | 1 | 5 | 2 | |||
| dp[*][1] | 3 | 1 | 1 | 5 | 7 | 6 | 2 | |
| dp[*][0] | 4 | 3 | 1 | 5 | 7 | 8 | 6 | 2 |
写一组数据,自己动手模拟一遍就可以理解咯~
预处理
根据状态转移方程,首先指定当区间长度为 $2^0$ 时的各初始值,随后推出后面的结果。
void ST_Init(const vector<int> &A)
{
int n=A.size();
for(int i=0; i<n; i++)
dp[i][0]=A[i];
for(int j=1; (1<<j)<=n; j++)
for(int i=0; i+(1<<j)<=n; i++)
dp[i][j]=min(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}
查询
预处理出整个 dp 数组以后,查询操作很简单,令 k 为满足 $2^k<=R-L+1$ 的最大整数,则以 L 开头、以 R 结尾的两个长度为 $2^k$ 的区间合起来即覆盖了查询区间 [L,R] 。
int RMQ(int L,int R)
{
int k=0;
while((1<<(k+1))<=R-L+1)k++;
return min(dp[L][k],dp[R-(1<<k)+1][k]);
}
线段树
嗯!怎么说呢?感觉线段树在这种类型的题目中好像是最万能的方法了。
无论是 [点修改 + 查询] 还是 [区间修改 + 查询] ,它都可以做到 $O(\log n)$ 的复杂度,而且在线段树中我们也可以维护好多好多东西(区间和、最值等)。
当然,除了一维情况下的普通线段树,还有在二维平面中的线段树,类似的也可以实现三维、四维。。。(啊!千千你要做什么o((>ω< ))o)
好啦~
对于一维中的线段树,我们想要查询某个区间的最值,首先就应该建树咯~(具体方法省略)
而在查询时,我们可以从根节点向下递归搜索,如下图,假设查询区间为 [2,6] 。
将 [2,6] 这一个大区间分解为不相交的三个小区间 [2,3]、[4,5]、[6] ,而最终的结果便由这三个节点中所维护的信息决定咯!
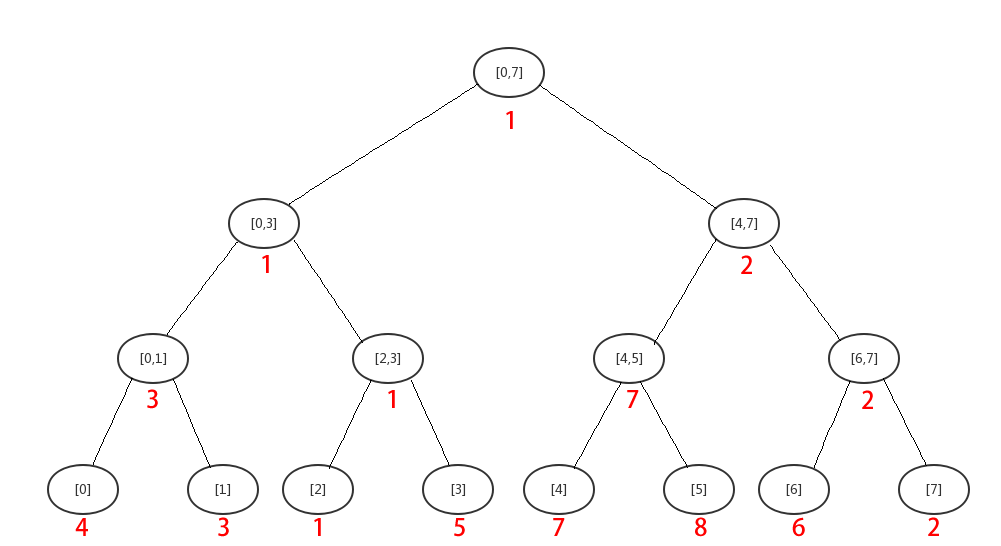
我们假设查询还是区间最小值,于是最终的结果为 $\min (1,7,6)=1$
线段树可以解决普通的 [点/区间] 修改 + 查询 ,当然它也可以解决 树中的路径权值 修改 + 查询(树链剖分)。
线段树:虽然我代码长,但是我功能强大呀~~~(〃` 3′〃)
千千:万一某天千千找到了更好的解法怎么办呢?
剧透:树链剖分其实是把一棵树剖分成很多链存储在一维空间中(压缩、压缩、压缩),然后最后的解法和一维线段树就变的一样咯。(干嘛说出来呀我~)
RMQ 标准算法
待定-ing




棒棒!网站优秀
你依然可以在我这里寻找图片的说。
被发现了,怎么办,好紧张o( ̄ヘ ̄o#) 会不会怪罪千千,呀!(逃
依然可以的说,不介意的。我在Pixiv找图片也找了蛮久的。
以后我也在 Pixiv 上找找 ,谢谢啦~
,谢谢啦~
虽然学过资料结构,但是都忘了
既然学过,再看的话就很轻松啦~