| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 8457 | Accepted: 4019 |
Description
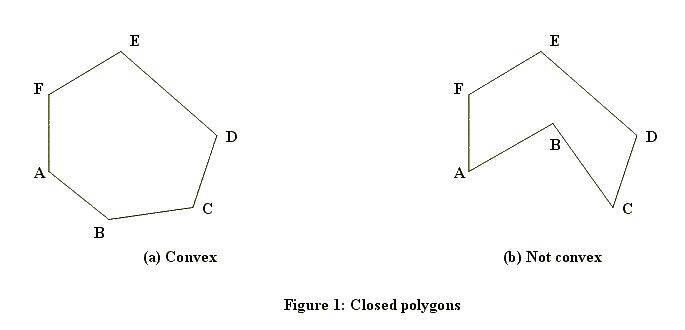
A closed polygon is a figure bounded by a finite number of line segments. The intersections of the bounding line segments are called the vertices of the polygon. When one starts at any vertex of a closed polygon and traverses each bounding line segment exactly once, one comes back to the starting vertex.A closed polygon is called convex if the line segment joining any two points of the polygon lies in the polygon. Figure 1 shows a closed polygon which is convex and one which is not convex. (Informally, a closed polygon is convex if its border doesn’t have any “dents”.)
The first property is that the vertices of the polygon will be confined to three or fewer of the four quadrants of the coordinate plane. In the example shown in Figure 2, none of the vertices are in the second quadrant (where x < 0, y > 0).
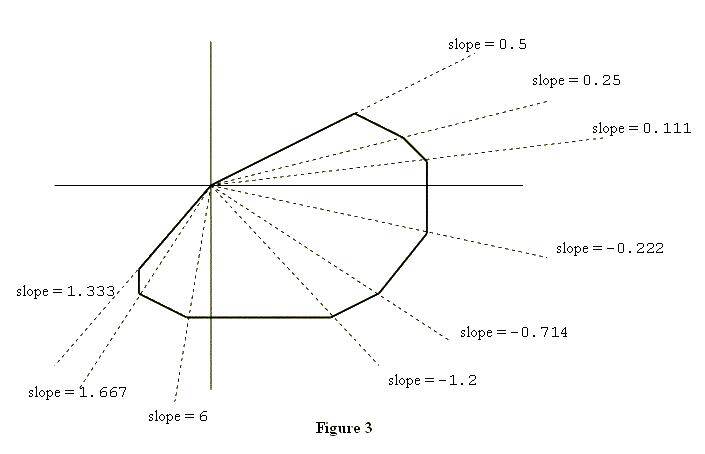
To describe the second property, suppose you “take a trip” around the polygon: start at (0, 0), visit all other vertices exactly once, and arrive at (0, 0). As you visit each vertex (other than (0, 0)), draw the diagonal that connects the current vertex with (0, 0), and calculate the slope of this diagonal. Then, within each quadrant, the slopes of these diagonals will form a decreasing or increasing sequence of numbers, i.e., they will be sorted. Figure 3 illustrates this point.

Input
Output
Sample Input
0 0
70 -50
60 30
-30 -50
80 20
50 -60
90 -20
-30 -40
-10 -60
90 10
Sample Output
(0,0)
(-30,-40)
(-30,-50)
(-10,-60)
(50,-60)
(70,-50)
(90,-20)
(90,10)
(80,20)
(60,30)
题意:给出一些点,将这些点进行极角排序后输出
AC代码:
#include <iostream>
#include<stdio.h>
#include<algorithm>
using namespace std;
struct point
{
int x;
int y;
} p[10010];
bool camp(point a,point b)
{
if((a.x*b.y-a.y*b.x)>0)
return true;
return false;
}
int main()
{
int n=0,i;
while(~scanf("%d %d",&p[n].x,&p[n].y))
{
n++;
}
sort(p+1,p+n,camp);
for(i=0; i<n; i++)
printf("(%d,%d)\n",p[i].x,p[i].y);
return 0;
}


很想知道,你这都学的是个啥?……
算法呀