POJ 1925 Spiderman （DP）

Description

Dr. Octopus kidnapped Spiderman’s girlfriend M.J. and kept her in the West Tower. Now the hero, Spiderman, has to reach the tower as soon as he can to rescue her, using his own weapon, the web.

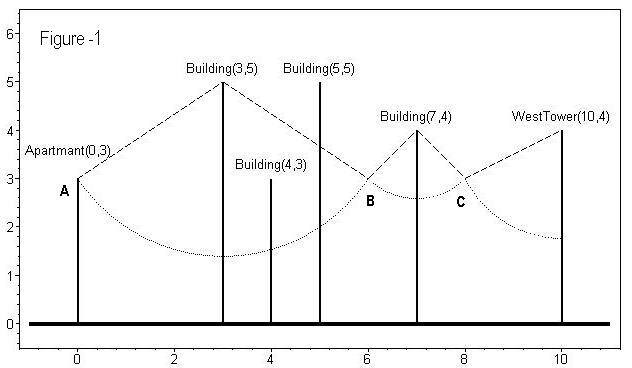
From Spiderman’s apartment, where he starts, to the tower there is a straight road. Alongside of the road stand many tall buildings, which are definitely taller or equal to his apartment. Spiderman can shoot his web to the top of any building between the tower and himself (including the tower), and then swing to the other side of the building. At the moment he finishes the swing, he can shoot his web to another building and make another swing until he gets to the west tower. Figure-1 shows how Spiderman gets to the tower from the top of his apartment – he swings from A to B, from B to C, and from C to the tower. All the buildings (including the tower) are treated as straight lines, and during his swings he can’t hit the ground, which means the length of the web is shorter or equal to the height of the building. Notice that during Spiderman’s swings, he can never go backwards.

You may assume that each swing takes a unit of time. As in Figure-1, Spiderman used 3 swings to reach the tower, and you can easily find out that there is no better way.

Input

The first line of the input contains the number of test cases K (1 <= K <= 20). Each case starts with a line containing a single integer N (2 <= N <= 5000), the number of buildings (including the apartment and the tower). N lines follow and each line contains two integers Xi, Yi, (0 <= Xi, Yi <= 1000000) the position and height of the building. The first building is always the apartment and the last one is always the tower. The input is sorted by Xi value in ascending order and no two buildings have the same X value.

Output

For each test case, output one line containing the minimum number of swings (if it’s possible to reach the tower) or -1 if Spiderman can’t reach the tower.

Sample Input

2
6
0 3
3 5
4 3
5 5
7 4
10 4
3
0 3
3 4
10 4

Sample Output

3
-1

题意

给出 n 个建筑，每个建筑以两个整数 x,y 表示， x 代表它在横轴上的位置， y 代表它的高度，所有的建筑高度都大于等于第一个建筑的高度，并且建筑的输入顺序按照 x 从小到大排列。

蜘蛛侠在第一个建筑物上，他要去最后一个建筑救女朋友，每一次蜘蛛侠可以摇摆到关于建筑对称的位置，且丝线长度不能大于建筑物的高度，求到最后一个建筑的最小摇摆次数。

思路

dp[i] 代表他到 x 轴 i 的位置所需要的最少摇摆次数，则状态转移方程： dp[i]=min(dp[i],dp[j]+1)

对于每一个 i ，枚举在它后面并且可以到达 i 的位置 j 。

AC 代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
#define INF 0x3f3f3f3f
typedef __int64 LL;

int dp[1000010];
LL x[5010],y[5010];
int n;

void solve()
{
    memset(dp,INF,sizeof(dp));
    dp[x[0]]=0;
    for(int i=1; i<n; i++)
    {
        int l=sqrt(y[i]*y[i]-(y[i]-y[0])*(y[i]-y[0]));  //计算对于建筑i来说所能接受的最远距离
        for(int j=max(x[0],x[i]-l); j<x[i]; j++)
        {
            if(dp[j]==INF)continue;
            int k=min(x[n-1],2*x[i]-j);
            dp[k]=min(dp[k],dp[j]+1);
        }
    }
    printf("%d\n",dp[x[n-1]]==INF?-1:dp[x[n-1]]);
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&n);
        for(int i=0; i<n; i++)
            scanf("%I64d%I64d",x+i,y+i);
        solve();
    }
    return 0;
}