Expanding Rods
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 15745 | Accepted: 4185 |
Description
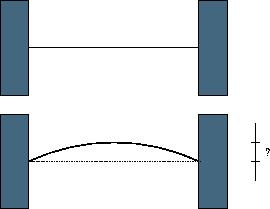 When a thin rod of length L is heated n degrees, it expands to a new length L’=(1+n*C)*L, where C is the coefficient of heat expansion.
When a thin rod of length L is heated n degrees, it expands to a new length L’=(1+n*C)*L, where C is the coefficient of heat expansion.When a thin rod is mounted on two solid walls and then heated, it expands and takes the shape of a circular segment, the original rod being the chord of the segment.Your task is to compute the distance by which the center of the rod is displaced.
Input
The input contains multiple lines. Each line of input contains three non-negative numbers: the initial lenth of the rod in millimeters, the temperature change in degrees and the coefficient of heat expansion of the material. Input data guarantee that no rod expands by more than one half of its original length. The last line of input contains three negative numbers and it should not be processed.
Output
For each line of input, output one line with the displacement of the center of the rod in millimeters with 3 digits of precision.
Sample Input
1000 100 0.0001
15000 10 0.00006
10 0 0.001
-1 -1 -1
Sample Output
61.329
225.020
0.000
题意
木棒受热膨胀后形成弧形,求它的最高点与原来水平之间的距离。
思路
我们假设弧所对应的半径为r,圆心角为2*s,弧长为L,弦长为l。
已知,弧长 L=r∗2*s , 且 L=(1+n∗C)∗l
弦长 l=2∗r∗sin(s)
两式消去s可得 L=2∗r∗arcsin(l/(2∗r))
另外,在图中存在这样的关系: r^2−(r−h)^2=(l/2)^2
化简得: r=(4*h^2+l^2)/(8*h)
这是一个超越方程,不会解怎么办,试呗!
两个式子合成一个便是
L=(4*h^2+l^2)*arcsin(4*h*l/(4*h^2+l^2))/(4*h)
用二分的方法逐一验证,不过二分只适用于单调的函数怎么办,这个函数是这种类型么?
于是,现场画一个图看看
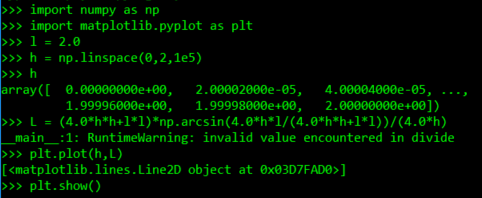
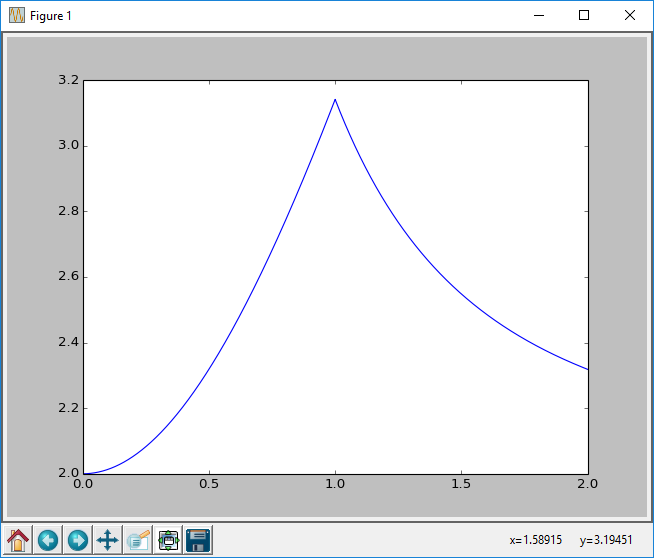
这里假设 l=2 ,绘制的图像范围是 [0,2]
但是因为h的取值只能是 [0,l/2] ,所以它在这个区间是一个单调递增的函数,于是二分法可用。
AC 代码
#include <iostream>
#include<stdio.h>
#include<math.h>
#define maxx (1<<25)
using namespace std;
int main()
{
double l,c,n;
while(~scanf("%lf%lf%lf",&l,&n,&c))
{
if(l<0||n<0||c<0)break;
double L=(1.0+n*c)*l;
double low=0,high=0.5*l,mid;
while(high-low>1e-7)
{
mid=(low+high)*.5;
double r=((4.0*mid*mid)+l*l)/(8.0*mid);
double as=2.0*r*asin(l/(2.0*r));
if(as>L)high=mid;
else if(as<L)low=mid;
else break;
}
printf("%.3f\n",mid);
}
}


验证函数单调性还可以给它求导,那么复杂的式子,我可不想试