POJ 1459 Power Network (最大流)

Description

A power network consists of nodes (power stations, consumers and dispatchers) connected by power transport lines. A node u may be supplied with an amount s(u) >= 0 of power, may produce an amount 0 <= p(u) <= p_max(u) of power, may consume an amount 0 <= c(u) <= min(s(u),c_max(u)) of power, and may deliver an amount d(u)=s(u)+p(u)-c(u) of power. The following restrictions apply: c(u)=0 for any power station, p(u)=0 for any consumer, and p(u)=c(u)=0 for any dispatcher. There is at most one power transport line (u,v) from a node u to a node v in the net; it transports an amount 0 <= l(u,v) <= l_max(u,v) of power delivered by u to v. Let Con=Σ_uc(u) be the power consumed in the net. The problem is to compute the maximum value of Con.

An example is in figure 1. The label x/y of power station u shows that p(u)=x and p_max(u)=y. The label x/y of consumer u shows that c(u)=x and c_max(u)=y. The label x/y of power transport line (u,v) shows that l(u,v)=x and l_max(u,v)=y. The power consumed is Con=6. Notice that there are other possible states of the network but the value of Con cannot exceed 6.

Input

Output

Sample Input

2 1 1 2 (0,1)20 (1,0)10 (0)15 (1)20
7 2 3 13 (0,0)1 (0,1)2 (0,2)5 (1,0)1 (1,2)8 (2,3)1 (2,4)7
         (3,5)2 (3,6)5 (4,2)7 (4,3)5 (4,5)1 (6,0)5
         (0)5 (1)2 (3)2 (4)1 (5)4

Sample Output

15
6

题意

这道题题目好长，好难懂哎！看了好久的题目。

先附上翻译(网上找的)

题目描述

一个电网包含一些结点（电站、消费者、调度站），这些结点通过电线连接。每个结点 u 可能被供给 s(u) 的电能， s(u)≥0 ，同时也可能产生 p(u) 的电能， 0≤p(u)≤pmax(u) ，站点 u 还有可能 消费 c(u) 电能， 0≤c(u)≤min( s(u),cmax(u)) ，可能传输 d(u) 的电能， d(u) = s(u) + p(u) – c(u) 。

以上这些量存在以下限制关系:

对每个电站， c(u) = 0 。对每个消费者， p(u) = 0 。对每个调度站， p(u) = c(u) = 0 。

在电网中两个结点 u 和 v 之间最多有一条电线连接。从结点 u 到结点 v 传输 L(u,v) 的电能， 0≤L(u,v)≤Lmax(u,v) 。定义 Con 为 c(u) 的总和，表示电网中消费电能的总和。本题的目的是求 Con 的最大值。

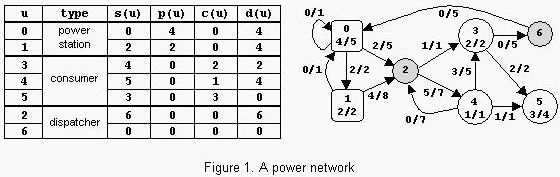
在图(a)中，电站结点 u 的标记” x/y ”代表 p(u) = x 、 pmax(u) = y 。消费者结点 u 的标记” x/y ”代表 c(u) = x 、 cmax(u) = y 。每条电线所对应的边 (u,v) ，其标记” x/y ” 代表 L(u,v) = x 、 Lmax(u,v) = y 。

在图(b)中，消费的最大电能 Con = 6 ，图(a)列出了在此状态下各 个站点的 s(u) 、 p(u) 、 c(u) 和 d(u) 。注意，如图(b)所示的电网中，电能的流动还存在其他状态，但 消费的电能总和不超过6。

输入描述

输入文件中包含多个测试数据，每个测试数据描述了一个电网。每个测试数据的第1 行为4 个整数： n,np,nc,m ，其中， 0≤n≤100 ，代表结点数目； 0≤np≤n ，代表电站数目； 0≤nc≤n ， 代表消费者数目； 0≤m≤n2 ，代表传输电线的数目。接下来有 m 个三元组， (u,v)z ，其中 u 和 v 为结点序号（结点序号从0开始计起）， 0≤z≤1000 ，代表 Lmax(u,v) 的值。接下来有 np 个二元 组， (u)z ，其中 u 为电站结点的序号， 0≤z≤10000 ，代表 pmax(u) 的值；每个测试数据的最后是 nc 个二元组， (u)z ，其中 u 为消费者结点的序号， 0≤z≤10000 ，代表 cmax(u) 的值。所有数据都是整数。除三元组 (u,v)z 和二元组 (u)z 中不含空格外，输入文件中其他位置允许出现空格。测试 数据一直到文件末尾。

思路

建立一个超级源点，发电站所提供的电量可以看做是从超级源点与发电站之间边的容量，同样建立一个超级汇点，消费者所消耗的电量可以看做是从它与超级汇点之间边的容量，对于三元组，u到v可以传输的电量便可以看做u到v之间一条容量为z的边。

最后求从超级源点到超级汇点之间的最大流即可。

AC代码

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<vector>
#include<queue>
using namespace std;

const int MAXN = 110;
const int MAXM = 110*110*2;
const int INF = 0x3f3f3f3f;

struct edge
{
    int v,f;    //边终点与当前流量
    int next;   //下一个兄弟位置
} edge[MAXM];

int n,np,nc,m;
int index;
int head[MAXN];
int level[MAXN];

void init()
{
    index =0;
    memset(head,-1,sizeof(head));
}

void addedge(int u,int v,int f) //同时往图中添加原边与反向边
{
    edge[index].v=v;
    edge[index].f=f;
    edge[index].next=head[u];
    head[u]=index++;
    edge[index].v=u;
    edge[index].f=0;
    edge[index].next=head[v];
    head[v]=index++;
}

int bfs(int s,int t)    //利用bfs搜索当前残量图中是否存在s到t的路径
{
    memset(level,0,sizeof(level));  //level为从源点到当前点的距离
    level[s]=1;
    queue<int>q;
    q.push(s);
    while(!q.empty())
    {
        int x=q.front();
        q.pop();
        if(x==t)return 1;
        for(int e=head[x]; e!=-1; e=edge[e].next)  //遍历所有与u临接的点
        {
            int v=edge[e].v,f=edge[e].f;
            if(!level[v]&&f)
            {
                level[v]=level[x]+1;    //广度优先搜索下一层距离源点比当前多1
                q.push(v);
            }
        }
    }
    return 0;
}

int dfs(int s,int maxf,int t)
{
    if(s==t)return maxf;    //找到一条路径，返回当前路径中的最小流量
    int ret=0;
    for(int e=head[s]; e!=-1; e=edge[e].next)   //遍历s所有邻接的点
    {
        int v=edge[e].v,f=edge[e].f;
        if(level[s]+1==level[v]&&f) //如果新点可达并且标号为允许弧
        {
            int minn=min(maxf-ret,f);
            f=dfs(v,minn,t);
            edge[e].f-=f;
            edge[e^1].f+=f;
            ret+=f;
            if(ret==maxf)return ret;
        }
    }
    return ret;
}

int dinic(int s,int t)
{
    int ans=0;
    while(bfs(s,t)) //先确定是否存在路径从s到t
        ans+=dfs(s,INF,t);  //
    return ans;
}

int main()
{
    while(~scanf("%d%d%d%d",&n,&np,&nc,&m)) //n作为源点，n+1作为汇点
    {
        init();
        int ai,bi,ci;
        for(int i=0; i<m; i++)  //ai到bi最大传输量为ci
        {
            while(getchar()!='(');
            scanf("%d%*c%d%*c%d",&ai,&bi,&ci);
            addedge(ai,bi,ci);
        }
        for(int i=0; i<np; i++) //ai最大发电量为bi
        {
            while(getchar()!='(');
            scanf("%d%*c%d",&ai,&bi);
            addedge(n,ai,bi);
        }
        for(int i=0; i<nc; i++) //ai最大消耗量为bi
        {
            while(getchar()!='(');
            scanf("%d%*c%d",&ai,&bi);
            addedge(ai,n+1,bi);
        }
        printf("%d\n",dinic(n,n+1));
    }
    return 0;
}