Leetcode 1391 检查网格中是否存在有效路径（bfs）

Description

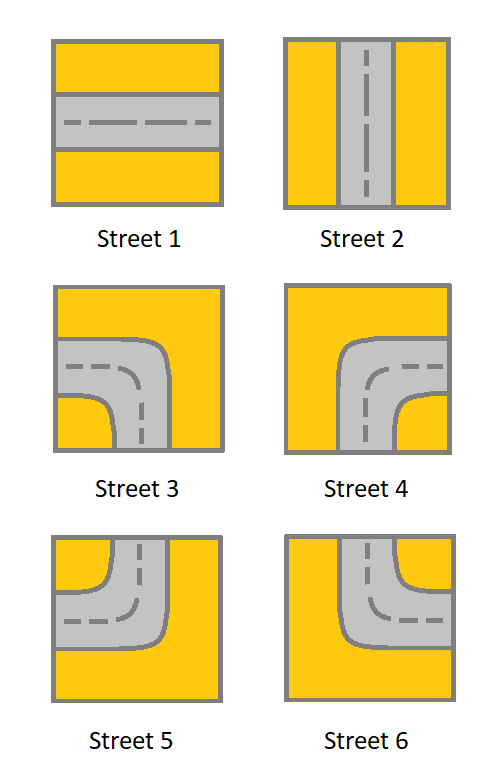
给你一个 m x n (1 <= m, n <= 300) 的网格 grid。网格里的每个单元都代表一条街道。grid[i][j] 的街道可以是：

1 表示连接左单元格和右单元格的街道。

2 表示连接上单元格和下单元格的街道。

3 表示连接左单元格和下单元格的街道。

4 表示连接右单元格和下单元格的街道。

5 表示连接左单元格和上单元格的街道。

6 表示连接右单元格和上单元格的街道。

你最开始从左上角的单元格 (0, 0) 开始出发，网格中的「有效路径」是指从左上方的单元格 (0, 0) 开始、一直到右下方的 (m-1, n-1) 结束的路径。该路径必须只沿着街道走。

注意：你不能变更街道。

如果网格中存在有效的路径，则返回 true，否则返回 false 。

Example input

grid = [[2,4,3],[6,5,2]]

Example Output

true

Example Hint

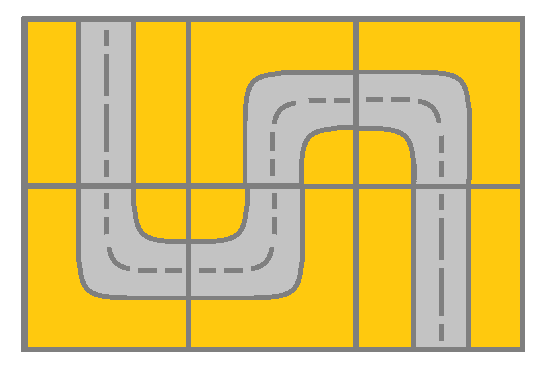
如图所示，你可以从 (0, 0) 开始，访问网格中的所有单元格并到达 (m - 1, n - 1)。

思路

首先，数据范围 $1 \le m, n \le 300$，如果遍历所有共 $300 \times 300$ 个点，不算很大。

再观察观察原先的图，每一种类型的 street 可以用一个 $3 \times 3$ 的矩阵来表示，且矩阵中只有三个点为 $1$，其余都为 $0$。

也就是说，如果我们考虑将整个地图还原出来，最大可能的地图大小为 $900 \times 900$，且其中只有 1/3 的位置可访问，一共 $900 \times 900 \div 3 = 270000$ 个点。

看似使用 bfs 暴搜 1s 的时间戳戳有余。那就搜吧，这样就 AC 了。

PS：Leetcode 很坑的地方就是这里，题目不会告诉你时间限制，也不会告诉你数据组数，但提交所计算的时间是在所有数据中执行时间的总和。曾经因为这个原因吃过很多亏，不知道有没有好心人告诉一下内部机制哇。

AC 代码

typedef long long LL;
typedef pair<int, int> P;
const int maxn = 1e5 + 10;
const int mod = 1e9 + 7;
const double eps = 1e-8;

int mapping[8][3][3] = {
    {{0, 0, 0}, {0, 0, 0}, {0, 0, 0}}, {{0, 0, 0}, {1, 1, 1}, {0, 0, 0}},
    {{0, 1, 0}, {0, 1, 0}, {0, 1, 0}}, {{0, 0, 0}, {1, 1, 0}, {0, 1, 0}},
    {{0, 0, 0}, {0, 1, 1}, {0, 1, 0}}, {{0, 1, 0}, {1, 1, 0}, {0, 0, 0}},
    {{0, 1, 0}, {0, 1, 1}, {0, 0, 0}}};
const int mv[4][2] = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
class Solution {
public:
    map<P, bool> vis;
    vector<vector<int>> res_grid;
    void init(vector<vector<int>> &grid) {
        int n = grid.size();
        int m = grid[0].size();
        res_grid.clear();
        for (int i = 0; i < n * 3; i++) {
            res_grid.push_back(vector<int>());
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                for (int k1 = 0; k1 < 3; k1++) {
                    for (int k2 = 0; k2 < 3; k2++) {
                        res_grid[i * 3 + k1].push_back(
                            mapping[grid[i][j]][k1][k2]);
                    }
                }
            }
        }
    }
    bool bfs(vector<vector<int>> &grid) {
        int n = res_grid.size();
        int m = res_grid[0].size();
        // cout << n << " " << m << endl;
        vis.clear();
        queue<P> que;
        que.push(P(1, 1));
        vis[P(1, 1)] = true;
        while (!que.empty()) {
            P front = que.front();
            que.pop();

            int xi = front.first;
            int yi = front.second;
            if (xi == n - 2 && yi == m - 2) {
                // cout << xi << " " << yi << endl;
                return true;
            }

            for (int i = 0; i < 4; i++) {
                int xx = xi + mv[i][0];
                int yy = yi + mv[i][1];
                if (xx < 0 || yy < 0 || xx >= n || yy >= m ||
                    res_grid[xx][yy] == 0 || vis.count(P(xx, yy)))
                    continue;
                // cout << xx << " " << yy << endl;
                que.push(P(xx, yy));
                vis[P(xx, yy)] = true;
            }
        }
        return false;
    }
    bool hasValidPath(vector<vector<int>> &grid) {
        init(grid);
        return bfs(grid);
    }
};