描述
小Hi最近在教邻居家的小朋友小学奥数,而最近正好讲述到了三阶幻方这个部分,三阶幻方指的是将1~9不重复的填入一个3*3的矩阵当中,使得每一行、每一列和每一条对角线的和都是相同的。
三阶幻方又被称作九宫格,在小学奥数里有一句非常有名的口诀:“二四为肩,六八为足,左三右七,戴九履一,五居其中”,通过这样的一句口诀就能够非常完美的构造出一个九宫格来。
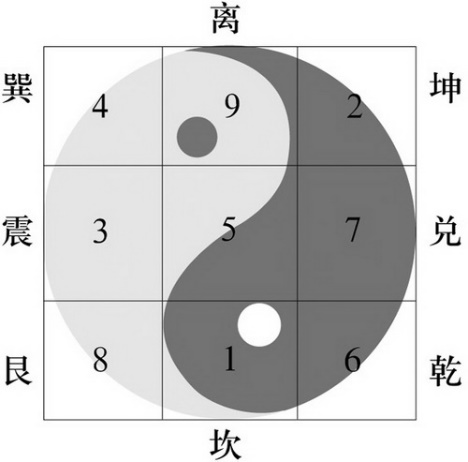
有意思的是,所有的三阶幻方,都可以通过这样一个九宫格进行若干镜像和旋转操作之后得到。现在小Hi准备将一个三阶幻方(不一定是上图中的那个)中的一些数组抹掉,交给邻居家的小朋友来进行还原,并且希望她能够判断出究竟是不是只有一组解。
而你呢,也被小Hi交付了同样的任务,但是不同的是,你需要写一个程序~
输入
输入仅包含单组测试数据。
每组测试数据为一个3*3的矩阵,其中为0的部分表示被小Hi抹去的部分。
对于100%的数据,满足给出的矩阵至少能还原出一组可行的三阶幻方。
输出
如果仅能还原出一组可行的三阶幻方,则将其输出,否则输出“Too Many”(不包含引号)。
样例输入
0 7 2
0 5 0
0 3 0
样例输出
6 7 2
1 5 9
8 3 4
题意
给出一个不完整的三阶幻方,问能否将它还原,如果可以还原成多种情况,输出 Too Many ,否则输出唯一还原后的幻方。
思路
怎么说呢!这道题,想了想这样的三阶幻方,中心的数字一定是5,并且四个角一定是偶数,不论怎么旋转变化,总共也不超过10种情况。
于是,很轻松的写出了八种所有情况。
接下来便是把输入的不完整幻方与所有的情况对比,若符合多个,便说明还原之后的幻方不唯一,否则输出可以还原到的幻方。
AC 代码
#include <iostream>
#include<stdio.h>
#include<stdlib.h>
#include<queue>
#include<string.h>
using namespace std;
int a[8][3][3]= //三阶幻方旋转总共只有八种情况,可以很快写出来的
{
{
{8,1,6},
{3,5,7},
{4,9,2}
},
{
{6,1,8},
{7,5,3},
{2,9,4}
},
{
{4,9,2},
{3,5,7},
{8,1,6}
},
{
{2,9,4},
{7,5,3},
{6,1,8}
},
{
{6,7,2},
{1,5,9},
{8,3,4}
},
{
{8,3,4},
{1,5,9},
{6,7,2}
},
{
{2,7,6},
{9,5,1},
{4,3,8}
},
{
{4,3,8},
{9,5,1},
{2,7,6}
}
};
bool judge(int a[3][3],int s[3][3])
{
for(int i=0; i<3; i++)
for(int j=0; j<3; j++)
if(s[i][j]!=0&&a[i][j]!=s[i][j])
return false;
return true;
}
int main()
{
int s[3][3],count=0,sk;
for(int i=0; i<3; i++)
for(int j=0; j<3; j++)
scanf("%d",&s[i][j]);
for(int i=0; i<8; i++)
if(judge(a[i],s))
{
sk=i;
count++;
}
if(count==1)
for(int i=0; i<3; i++)
for(int j=0; j<3; j++)
printf(j!=2?"%d ":"%d\n",a[sk][i][j]);
else printf("Too Many\n");
return 0;
}


